繰り返し計算におけるCの初期値はどのように決めたら良いでしょうか?
様々な方法が提案されていますが[1]、ここではEvolving Factor Analysisを使用します。2.1. 主成分数の決定で説明した特異値σを活用します。
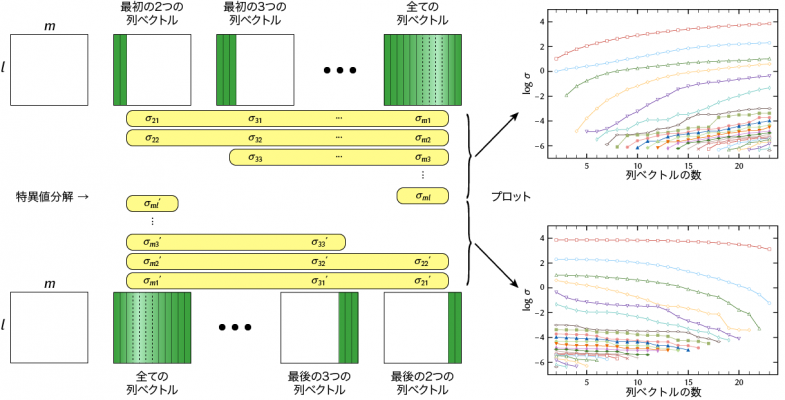
- 解析をするl×m行列の最初の2つの列ベクトルについて特異値分解を行い、特異値を求めます。
- 列ベクトルの数を1ずつ増やして特異値を求めます。
- 全ての列ベクトルでの特異値がもとまったら、それぞれで求めた特異値をつなげてプロットします。
- 次に同じ作業を逆方向で行います。
特異値は、2.1. 主成分数の決定で説明したように各成分の重要度を示します。幾つの成分で元の行列が再現できるか、という情報が特異値の大きさで表現されます。この性質を利用して、ある試料の中に存在する成分の個数を予測します。
この例では、成分数を4と予測しています(2.1. 主成分数の決定)。ということで、上図で求めた順方向、逆方向のプロットの内、それぞれ大きい方から4つのプロットを抜き取ります。順方向で最も大きいプロット、逆方向で最も小さいプロットを組み合わせて、小さい方の値をつなげてプロットします。残り、順次組み合わせてプロットを作ります。これらをまとめたものを化学種分布Cの初期値とします。