成分分析では、最初に主成分の数、ここでは存在する化学種の数を決定します。主成分数の決定を間違うと、これ以降の解析は全くの無意味になってしまいます。
単純に数学的に観測データ行列Aを2つの行列の積の形に分解するには、特異値分解という行列分解を使います。l行m列の行列Aを特異値分解すると、次のように分解が存在します。
A = UΣV
行列Uの行ベクトルは各成分の濃度成分、行列Vの列ベクトルは成分ごとのモル吸光係数です。ここで、Σは行列Aの特異値σを対角成分に持つ行列で、各成分の重み付けの情報を持っています。
最も古典的な主成分数の決定方法は、特異値σを成分数の関数としてプロットする図を活用します。主要な成分以外は、実験などの誤差を再現する成分ですから、特異値σもおのずから小さくなります。また成分数に対する変化も小さくなる、すなわち傾きが大きく変化し、主成分数以降の傾きは、0に近づきます。
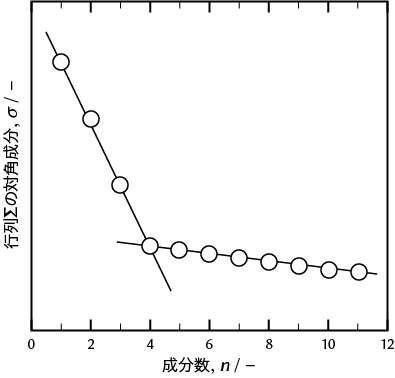 |
図1 主成分数が4である場合のプロット。
成分数4を境に傾きが変わる。 |
以上の方法を基に、主成分数の決定方法には、幾つかの方法が提案されています[1]。しかし、決定的な方法がありません。
そこで、特異値のσの変化ではなく、行列Uの行ベクトルあるいは行列Vの列ベクトルに着目して、新しい指針を提案しています[2]。
主要な成分以外の行列U、Vのベクトル成分は実験誤差を再現するためのものです。主要成分のベクトルは滑らかですが、実験誤差はランダムに現れる、すなわち、滑らかさを失うはずです。すなわち行列Uの行ベクトルの成分数に関する変化は次のようになります。
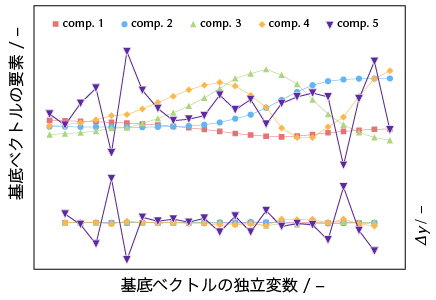 |
図2 上がベクトル成分の変化。
成分4までは滑らかだが、成分5は凹凸がある。 下のプロットは、ベクトル成分の微分成分Δy。 成分5の微分成分は、他の成分の微分成分に 比較して大きく、滑らかさが失われている ことが分かる。 |
上の例では、成分数4と5の差がはっきり分かりますが、この差が明確でない場合は、どうしたら良いでしょうか?
その場合、各成分の微分成分の絶対値|Δy|の総和あるいは平均を取って、プロットします。
 |
図3 図2のΔyの絶対値の平均プロット。
成分数5で平均値が大きくなっており、 成分数4までの回帰直線から大きく ずれていることが分かる。 |
このプロットだと傾きの変化がよりはっきり認識できます。
これまで提案されてきた主成分数の決定方法は、ここで提案している方法も含めて経験則に基づくものばかりです。解決すべき課題にあわせて、その都度適切な方法を選択するより他ありません。
判断に迷う場合は、可能性のある主成分数についてこれ以降の解析を全てテストし、最適な結果、モデルを選択するのが、最も確からしい方法であると考えています。
参考文献
[1] Paul Gemperline: Practical guide to chemometrics, (Taylor & Francis Group, Boca, Raton, FL, 2006)
[2] Masahito UCHIKOSHI, “Determination of the Distribution of Ferric Chloro Complexes in Hydrochloric Acid Solutions at 298 K,” Bulletin of the Chemical Society of Japan, 92(12), pp. 1928-1934, Dec. 2019, DOI: 10.1246/bcsj.20190195(解説はこちら)
※特異値分解等の数学的取り扱いに関しては、適切な教科書等を参照してください。また、記述に間違いがございましたら、masahito.uchikoshi.b5♣tohoku.ac.jp(クローバーを@に変換してお送りください)までお知らせ願います。