成分分析で解析するデータは、線形性を持つ特性の測定値です。その意味で、紫外可視吸収分光は解析に最適なデータです。
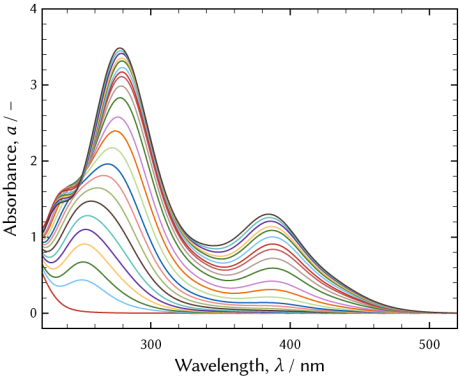
具体的には、例えば、一定濃度の金属イオンを含む塩酸濃度を変化させた一連の水溶液試料の紫外可視吸収分光を解析します。
吸収aλは、Lambert-Beerの法則に従います。λは観測波長です。
ここで、ελはモル吸光係数、cは溶質のモル濃度、lは光路長です。この式は、特定の波長における、一種類の溶質の吸収のみを考慮していますが、これを、N種類の溶質が共存する溶媒濃度を変化させた一連の試料溶液に拡張してみましょう。
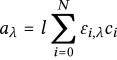
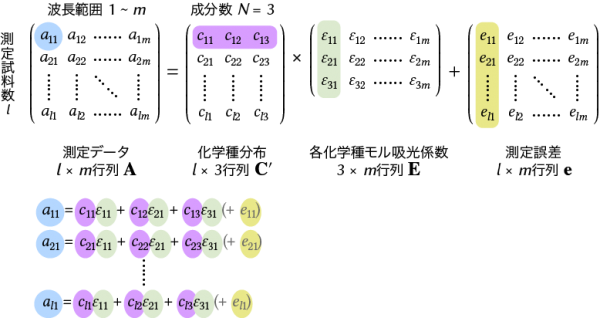
吸収は、線形性を有する特性なので、試料の吸収は各溶質の吸収の総和となります。この式を行列の形式に書き直すと、次のようになります。成分数（化学種の種類）を3と仮定して書いています。次の行列形式での表現には測定誤差の項eを追加しています。実際の測定には、この測定誤差がつきものです。
解析に適したデータを得るには、測定誤差を小さくすること、測定試料数を多くすること、測定波長範囲における吸収が同等の強度であることが求められます。特に測定試料数が化学種の種類よりも少ないと解析は原理的に不能となります。以上の点に注意してデータを取得します。
図 解析に使用する吸収スペクトルの例
必要に応じて、溶質イオン濃度による補正を行います。上記のように吸収はLambert-Beerの法則に従うので、各試料における溶質イオン濃度をキレート滴定法や誘導結合プラズマ発光分光分析法（ICP-OES）などで定量し、基準濃度における吸収強度に補正します。この補正をしておかないと、各試料の吸収スペクトルの変化が連続的とならず、解析に失敗します。
目次
3. 熱力学モデルの最適化
3.1. 熱力学モデルの構築
3.1.1. 活量の取り扱い
3.2. 最適化
3.3. 熱力学モデルの決定
4. 熱力学モデルの検証
4.1. X線吸収分光による錯体構造決定
4.2. 第一原理計算による検証