式の導出

０．平板−平板間の電気二重層を考える。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

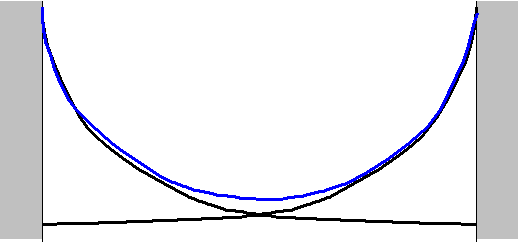１．まず、片側の二重層のみを考える

拡散層中のイオンの濃度はボルツマン分布に従う

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (1)

n: 拡散層中のイオンの個数濃度

n₀: バルク溶液中のイオンの個数濃度

z: イオンの価数

k: ボルツマン定数

T:　温度

y: 問題にしている点における電位

+,-: 陽イオン、陰イオンを表す

 

表面の電位：y0は電位決定イオンのバルク活量cによって、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2)

R: 気体定数

c₀: c at y₀ = 0

 

拡散層内における電位は、Poissonの式

　　　　　　　　　　　　　　　　　　　　　　　　　 (3)

を基礎にして求められる。

e_r: 溶液の比誘電率

e₀: 真空の誘電率

r: 電荷密度

は、対称型電解質（）に対して、

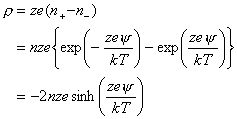　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (4)

従って、

平板電気二重層に対する、Poisson-Boltzmann式は、(3),(4)式からx方向だけを考えて

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (5)

(5)式を積分して、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (6)

 

なら、(5)式は、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (7)

ただし、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (8)

25℃水溶液では特に

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (9)

このκは、Debye-Huckelパラメータと呼ばれる。

 

(7)式を解くと、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (10)

 

一方、表面電荷密度sは電気性中性の原理から、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (11)

s_d: 底面が単位面積の液体柱に含まれる拡散層の全電荷

(4)式を使うと、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (12)

(10)、(12)から、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (13)

s₀の厳密解は、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (14)

 

2. 次に平板電気二重層間の相互作用を考える

溶液中の２枚の平行平板（板間距離: h）に作用する力Pは

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (15)

静電気成分　＋　浸透圧成分

（電気力線により内側に引かれる力）＋（対イオンの浸透圧により外側へ押される力）

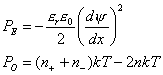　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (16)

P_Oは常にP_Eよりも大きく、板は反発力を受ける

板の接近過程で表面の電位y₀が変化しなければ、P_Eの寄与を無視して、(1)と(16)のP_Oの式から、板の受ける反発力P_R(h)は単位面積あたり

（このときの考え方は、２つの平板の丁度中間の面と無限遠の面を考え、中間の面上では、対称性から電場は零、無限遠の平面でも電場は零であるから、浸透圧成分のみを考えればよい、ということになる）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (17)

y_2/h: 板間の中央における電位

相互作用が弱ければ、y_h/2は単独の電気二重層の電位y_s(h/2)の２倍と考えて、

より、(6)式から、

（この近似は、後述するように、y<20 mVのとき成立する）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (18)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (19)

(17)式でより、これに(18)式を代入して、

（この近似は、kh>1、つまり、hが電気二重層の厚さよりも長いところで成り立つ

近似には cosh y @ 1 + y² を使用した）

すると、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (20)

 

従って、平板間の電気二重層の相互作用エネルギーは

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (21)

 

3. Derjaguin近似から球形粒子の相互作用力へ

Derjaguin近似: 半径a₁とa₂の球形粒子の最近接距離Hのとき

（H<<a₁,a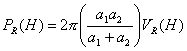₂）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (22)

(21)と(22)よりa₁=a₂=aのとき、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (23)

従って、半径aの球形粒子の相互作用エネルギーは

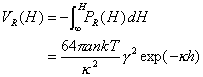　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (24)

いま、のとき、(23),(24)式は

（zey₀=4kTは、1:1電解質で25℃で、y₀=103 mVのとき成立、

y₀=20 mV以上では、zey₀/4kTとtanh{ zey₀/4kT}に、1%以上のずれが生じる

ので、20mV以下でこの近似は成り立つ）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (25)

　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 (26)

(13)式を使うと、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (27)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (28)

 

3. 全相互作用力、ポテンシャル

これらと、van der Waals力の近似式

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (29)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (30)

AはHamaker定数

をそれぞれ足しあわせると、全相互作用力、ポテンシャルとして、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (31)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (32)

が得られる。

あるいは、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (33)

であり、通常は、これらの式を使用する。

 

4. 式の意味を考えよう！

(33)式の第１項は、静電的反発力による反発エネルギー、第２項は引き合うエネルギーであり、両者の関係による最終的に、粒子同士が反発するかどうかが決まる。

第１項を支配するのは、exp内のκである。この数値によって、反発エネルギーの粒子間距離依存性が決まる。κは

と書けるので、

 

イオン濃度 nが増加すると、κは増加する

イオンの価数 zが増加すると、κは増加する

 

ことがわかり、結局、

 

イオン濃度 nが増加すると、同じ距離で比較した場合の反発エネルギーは減少する

イオンの価数 zが増加すると、同じ距離で比較した場合の反発エネルギーは減少する

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

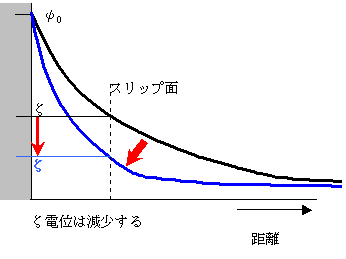図の赤い矢印方向に拡散二重層は圧縮する。つまり、スリップ面の電位＝ζ電位も減少する。ということは、実際にはある距離の電位が低くなることから、粒子は接近しやすくなることを意味している。